张祥前《统一场论第六版》

二十八.统一场论动量公式

1.静止物体周围空间的运动量。

我们考察一个物体o点，周围空间总是以圆柱状螺旋式在向外发散运动。

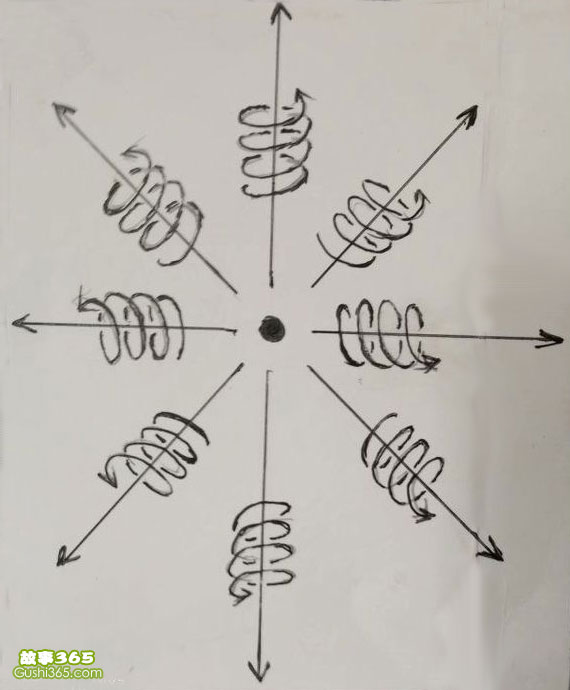
前面的三维螺旋时空方程告诉我们，空间的圆柱状螺旋式运动是由空间旋转运动位移Vt加旋转平面垂直方向的直线运动位移Ct的合成。

由于质点o静止时候周围空间运动的均匀性，旋转运动位移Vt会相互抵消为零，只是剩下了以矢量光速C的直线运动【如下图】。

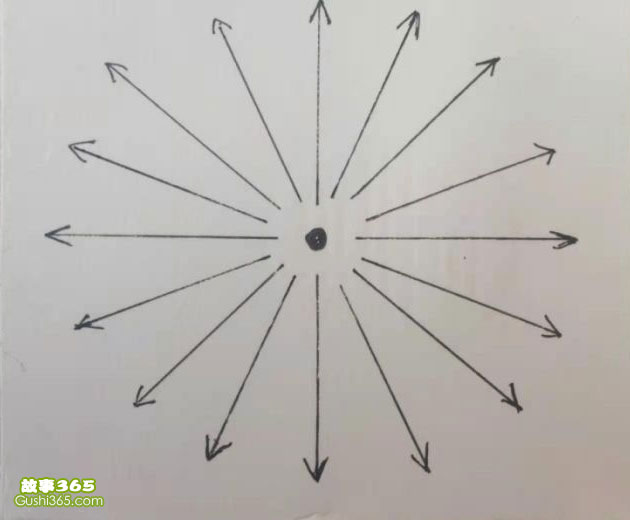
严格的证明和磁场的高斯定理类似。

设有一个物体o点，相对于我们观察者静止，其周围空间总共有n条几何点的位移R = Ct，因而其总的运动量：

L = n R= n Ct

2.物体的静止动量定义

以上的o点相对于我们观察者静止，将周围空间几何点总的运动量L = nR = nCt对立体角度Ω求偏导数，这里假定只有n随Ω变化。有：

∂L/ ∂Ω = [∂n/∂Ω]R = [∂n/∂Ω]Ct = m Ct

将上式对时间t求偏导数，这里只是考察Ct随时间t变化，而质量m不随时间变化，所得到的结果就是o点静止动量:

P静 = m C

o点的静止动量反映了o点周围立体角度4π内有n条几何点的矢量光速C。

我们虽然用o点周围空间某一个点p的运动程度来考察o点的静止动量，但是，o点周围空间总运动量L = n R = n Ct只是随立体角度Ω、时间t的变化而变化，不随【和我们观察者之间的】空间距离而变化，也不随p点和o点之间距离的变化而变化。

所以，我们测量一个物体o点静止动量的大小，不需要考虑o点离我们观察者有多远，也不需要考虑o点和周围一个考察点p之间距离。

当o点运动的时候，情况是类似的。

3.运动物体周围空间的运动量

我们第一步指出静止物体周围空间运动量，然后求出相对于这个物体匀速直线运动运动的另外一个观察者，测量出这个物体周围的空间运动量，这样可以求出运动物体周围的空间运动量。

在下图中，惯性参考系s’的原点o’点和s系的原点o在时刻为零的时候，相互重合在一起。

s’系相对于s系以匀速度V沿x轴或者x’轴正方向【x轴和x’轴相互重合】直线运动。

以上的物体o点，始终静止于s’系的原点o’处。

并且，s系的观察者始终处于s系里的原点o处；s’系的观察者始终处于s’系的原点o’处。

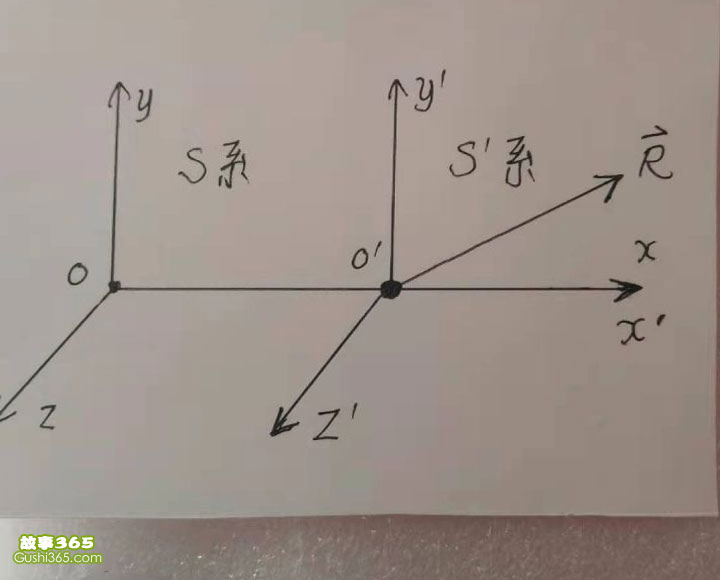
在s’系里观察，物体o点周围空间的一个几何点p，在0时刻从o’点出发，经过一段时间t’后，运动到p点现在所在的位置。

t’是s’系里的时间，为了区分，以后用t表示s系里的时间，用C和C’分别表示s系、s’系里几何点的矢量光速。

由o’点指向p点的几何点位移矢量为

R’ = C’t’= cN’t’。

p点处于R’的端点处，在上图中没有标出。

R’是几何点p在s’系里的光速运动位移。我们用R来表示s系里里几何点p的光速运动位移。

由于两个相互运动观察者测量同一束光的标量速度c是一样的【这个详细的证明百度统一场论6版】。

这样，在s系里观察者认为，几何点p相对于s系的观察者所在的原点o，其运动位移：

R = Ct= c N t

N是单位矢量。

在s系里观察者认为，几何点p相对于物体o点，其运动位移R – Vt，因为o点以速度V相对于s系里观察者在运动。

将R – Vt对时间t求导数，得到：是s系里，几何点p相对于物体o点的运动速度为：C - V

注意，p点相对于原点o的运动速度和相对于物体o点的运动速度之间的区别。

4.运动物体的动量

上面告诉我们，物体o点以速度V运动的时候，周围空间一个几何点p相对于物体o点速度为C – V，假定物体o点周围在立体角度n/4π内有n条C – V，

这样物体o点以速度V运动的时候，具有运动动量：

P动 = n/4π（C – V），

由质量的定义方程m = n/4π.上式可以改为：

P动 = m（C – V）

相对论力学、牛顿力学认为物体周围空间的光速运动不存在，也就是C = 0，所以，牛顿力学、相对论的动量方程是P动 = m V，也可以说相对论、牛顿力学的动量公式只是上式的一个分量。

这个动量公式只是把牛顿、相对论动量公式扩展了，包含了物体静止时候周围空间的光速运动。

5.物体运动时候的动量和静止时候的数量是相等的

将运动动量公式P动 = m（C – V）两边平方，结果为：

p² = m²（c ²– 2C·V + v²）

p为运动动量P的标量。

由第五节的式cosβ = v/c和C·V = v c cosβ = v²，可以把式p² = m²（c ²– 2C·V +v²）改写为：

p² = m²（c ²– v²）

p = mc√（1-v²/c²）

我们应该合理的认识到，一个物体的静止动量m’C’和运动动量m（C- V）的数量是相等的，不同的只是方向。

| m’C’| = | m（C - V） |

将上式两边平方，结果为：

如果物体运动时候的动量mc√（1 - v²/c²）和静止时候的动量m’c数量相等，

m’ ² c² = m²c²（1 - v²/c²）

两边开发，得：

m’c = mc√（1 - v²/c²）

上式两边同时除以标量光速c，就是相对论的质速关系方程m’ = m√（1 - v²/c²）。