张祥前《统一场论第六版》

五十.导出毕奥---萨伐尔定理

恒定的电流在其周围产生的磁场，其规律可以用毕奥---萨伐尔定理描述。

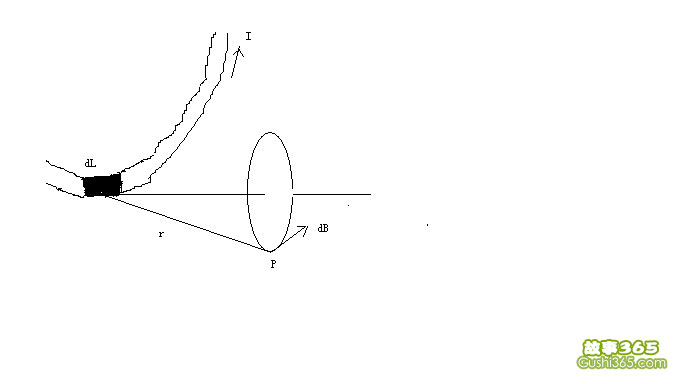
毕奥---萨伐尔定理表述如下：在一段导线中，有恒定的电流流过，dL表示这个导线中很小的一段，用i表示这一小段电流的电流强度。idL称为电流元，反映了这一段导线中截流子运动情况。

电流元在周围空间某处p点产生的磁场dB由下式决定：

dB = μ。idL×R/ 4 π r ³

= μ。idL×【R】/ 4 π r²

式中μ。为真空中磁导率，R【数量为r】为从电流元指向P点的矢径。【R】为沿R方向的单位矢量。

以上毕奥—萨伐尔定理是从实验中总结出来的规律，反映了运动电荷在周围空间产生的磁场情况。我们知道，磁场是电场的相对论效应，相对于我们观察者静止的电荷在周围空间产生静电场，一旦电荷相对于我们观察者以某一个速度运动，又会在周围空间产生磁场，应该可以用相对论导出毕奥---萨伐尔定理，下面来给出导出过程。

首先我们用式dB =μ。i dL×【R】/ 4π r²导出匀速运动点电荷的磁场。

在上图中的电流元，设它的截面为s，其中截流子数密度为n，每个截流子的电荷都是q，并且都以漂移速度V 运动，V的运动方向和dL的方向一致，整个电流元i dL在P点产生的磁场可以认为是这些以同样速度V运动的截流子在p点产生的磁场的叠加，由于电流强度i = n q s V, 而且此电流元内公有n s dL个截流子，所以，每一个截流子在p点产生的磁场B（忽略不同的截流子到p点的矢径的差异）就应该是：

B = μ。n q s V i dL×e【R】/ 4π r² n s dL

由于V和dL方向相同，所以有：

B = μ。q V×【R】/ 4 π r²

由相对论我们知道，一个以速度V相对于我们观察者匀速运动的点电荷，产生的磁场B和电场E、光速c满足以下关系：

B = V×E/c²

我们确定了式B = V×E/c²中电场E的分布，就可以做出判断，为此，我们利用库伦定理，

E = q 【R】/4 π ε。r²

由式E = q 【R】/4 π ε 。r²和式B = V×E/c²可以导出式

B = μ。q V×【R】/ 4 π r²

注意ε。μ。=1/ c²

我们知道，库伦定理导出的电场分布只适于静止电荷，不适于运动电荷，但是，导线中的截流子（就是导线中自由移动的电子）一般速度是很小的，只有0.0001米/秒，和光速c比起来简直是太小了，是可以忽略的。

磁场的安培环路定理可以从毕奥----萨伐尔定理导出来，而麦克斯韦的位移电流假说也反映了随时间变化的电场可以产生磁场，这一切和相对论中随速度变化的电场产生磁场本质都是一回事情。

一个物理量随速度变化，就意味着一定会随时间变化。把安培环路定理、毕奥----萨伐尔定理、麦克斯韦位移电流假说、相对论中磁场是电场的相对论效应综合起来考虑，更加深我们对自然界统一于时空、统一于运动的认识。