张祥前《统一场论第六版》

四十九.变化电磁场产生引力场

随时间变化的磁场产生引力场

统一场论核心是：随时间变化的引力场可以产生电磁场，随时间变化的电磁场也可以产生引力场。

这里介绍的是：随时间变化的磁场产生引力场情况。

相对论和电磁学认为，一个相对于我们观测者静止的点电荷o,在周围空间某处p点产生了静电场E, 当o点相对于我们观测者以速度V运动，o点在p处还产生了磁场B，p处的合场为E + V×B.其中E和B满足以下关系：

B = V×E/c²

传统的看法是物质点周围的空间与物质点是不相干的，统一场论把物质点周围空间与物质点的运动状态联系在一起。

统一场论认为，当以上的o点相对于我们观察者以速度V运动时候，我们观察者认为p处也有一个速度V 。p点在统一场论中被看成是几何点，当o点相对于我们以加速度A运动时候，p点也具有一个加速度A。这个加速度在统一场论中是几何点的加速度，而统一场论认为几何点的加速度就是引力场，由此认定p点的加速度A就是引力场。

当o点相对于我们加速运动，找到了p点的加速度A和电磁场E、B的关系，就找到了加速变化的电磁场和引力场之间的关系。

为此，我们将式B = V×E/c² 对时间t求导，有下式：

dB/dt = dV/dt ×E/c² + V×（d E / dt ）/c²

认定A是加速运动电荷o在p处产生一种由随时间变化的电磁场转化的引力场。

如果在这种情况下，电场E不随时间变化，或者说我们只考虑B 和V 随时间变化时相互对应关系，上式可以写为：

∂ B /∂t = A×E/c²

用语言描述上式是：随时间变化的磁场可以产生和磁场环绕的平面相垂直方向的引力场。这样，加速运动点电荷o在周围空间p处的引力场A’等于

A’ = A- A静

上式告诉我们，加速运动点电荷o周围空间p处的引力场A’ 包括：o静止本来就有万有引力场 -A 静和随时间变化的磁场产生的引力场A两部分。

o在p处产生的磁场B、引力场 A、电场E的关系dB/dt = A×E/c² 如下图所示填写图片摘要（选填）

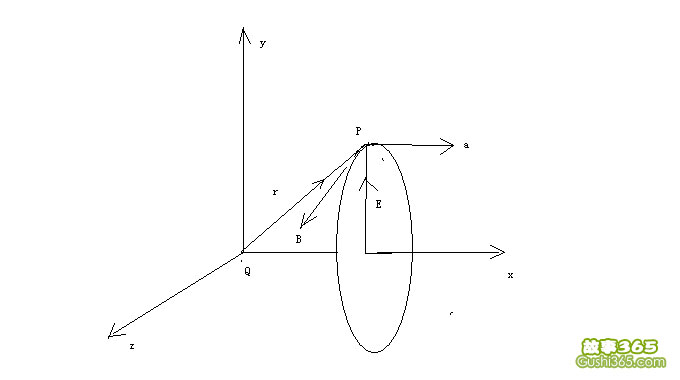
我们需要注意的是，由电磁场变化而产生的引力场是关于平面对称的，而万有引力产生的引力场是关于点对称的，这个是二者主要的区别，这个也是电磁场力产生的重引力力不能够直接和万有引力产生的引力场力相互作用的原因。

电磁场和引力场之间的关系，万变不离其宗，都是物质粒子周围空间相对于我们观测者不同的运动形式之间的关系。一句话，电磁场和引力场都是变化空间的不同形式。

现在我们来讨论一下任何利用变化电磁场产生引力场问题。

统一场论预言了：

1.穿过有限曲面的磁场发生变化的时候，产生磁场垂直方向的、沿曲面边缘线分布的环绕线性电场和引力场。并且，这个时候，在空间一点上，变化磁场、产生的电场、引力场三者相互垂直。

2.加速运动的负点电荷产生与加速度方向一致的连续分布的反引力场，并且产生了产生了加速度方向垂直的、对称分布的反引力场。

这种对称分布的反引力场可以抵消物体因万有引力而产生的引力场，进而使物体的质量消失。

3.匀速直线运动的点电荷，在运动速度垂直方向的平面上，产生了平面分布的引力场。

我们有个疑问，自然界有没有天然存在的反引力场物体？答案是没有的，设想我们太阳系附近有反引力场物体，这些物体和太阳、地球及其他星体相互排斥作用，若干年后，这些反引力物体会被挤出太阳系，这样的结果是宇宙中反引力物体将和普通引力场物体生活在不同的空间区域，各过各的日子，互不相干。

1.加速运动点电荷的变化电场产生引力场

设想一个相对于我们观测者静止的点电荷o,带有电量为q的正电荷，在o点周围空间中一个几何点d处，产生了静电场E

当o点相对于我们以加速度a加速运动，几何点d相应的会有一个加速度a ，按照前面引力场定义，几何点d所在的位置，会产生引力场 –a【矢量形式用A表示】。

我们来求出电场E、E的变化形式Eθ和引力场-a之间的关系。

现在设想点电荷o相对于我们观测者一直静止在笛卡尔坐标系的原点，从时刻t = 0开始以加速度A【数量为a】沿x轴正方向作直线加速度运动。

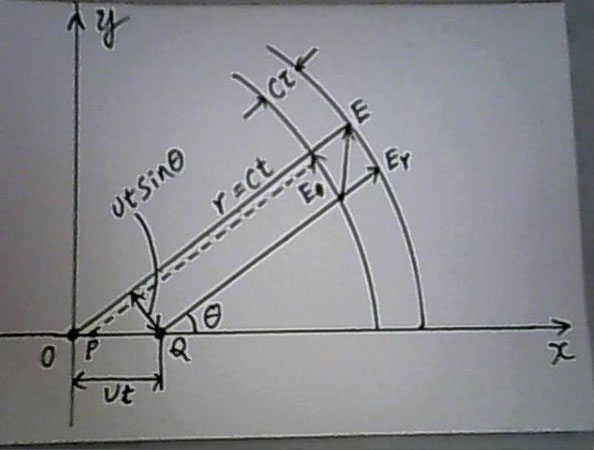
在时刻t =τ时，o点的速度达到了v = aτ,以后就以速度v继续作匀速直线运动。如下图所示：

为了简单起见，我们考虑的是v远远小于光速c，下面我们考虑在任意时刻t(t远大于τ)时电荷o周围的电场分布情况。

在0-τ这一段时间内，由于电荷o的加速运动，它周围的电场线会发生扭曲，并且这个扭曲状态会以光速c向外延伸，统一场论明确的指出，电场线就是电荷周围以光速运动的几何点的运动。

以上的扭曲状态以光速向外运动，这个就像一个向四周匀速喷水的水龙头，一旦水龙头抖动一下，引起水流发生扭曲，这个扭曲状态肯定的以水流的速度向外延伸。

在t=τ时候，点电荷o停止了加速，处于x轴上的p点，由加速运动电荷o引起的电场的扭曲状态以光速c向外延伸，在上图中可以看到扭曲状态厚度为cτ，夹在两个球面之间。

这两个球面其中的后一个球面，在t时刻已向四周传播了c（t-τ）这么远的距离，结果是以p点为中心，直径为c（t-τ）的球面。

这两个球面其中的前一个球面，在t时刻已向四周传播了ct这么远的距离，结果是以o点为中心，直径为ct的球面。

由于从时刻t=τ开始，电荷o作匀速运动，所以在这球面内的分布的电场应该是作匀速直线运动的电荷的电场。

根据我们前面的设定，电荷o的运动速度v远远的小于光速c,,所以这球面内的电场在任意时刻都近似为静电场。

在时刻t,这一电场的电场线是从此时刻o点所在位置Q引出的沿半径方向的直线。

由于t远大于τ，c远大于v，所以ct远大于1/2vτ(即从o点到p点的距离)。因此，扭曲状态的前、后沿的两个球面几乎是同心圆。

随着时间的推移，以上的扭曲状态的半径（ct）不断的扩大，以光速向外延伸、传播。

我们从电荷、电场定义方程知道，电场线发生扭曲，不会改变电场线的条数，所以在扭曲状态的前后两侧面的电场线的条数是相等的。

在v远小于c时候，这个扭曲的电场线可以当直线来看待。

我们选用与x轴成θ 角的那一条电场线来分析。

由于从o点到p点的距离op比r = ct要小得多，我们可以把o点和p点看作为一点(，也就是op接近于零)。

而oQ =vτ/2+v(t-τ) ≈ vt

扭曲区内的电场E可以分成两个分量Er【径向电场，本来就存在，其数量为er，】和Eθ【横向电场，可以看成是Er的变化形式】。

由上图可以看出

Eθ/er= vtsinθ/cτ= atsinθ/c = a r sinθ/c²

由于引力场可以用-a表示，我们用矢量A来表示引力场，所以有：

Eθ/er= -A×R/c²

上式中由o点指向几何点d的位置r =ct改用矢量R来表示。

上式也可以写为：

Eθ/er= R×A/c²

以上电场Eθ垂直与电磁场的传播方向（这里是Er的方向），并且只有在扭曲状态中存在，所以，它就是o电荷加速运动时候所产生的横向电场。Eθ可以看成是电荷因为加速运动引起了Er的变化。

上式给出了电荷o静止时候本来就存在的电场Er、加速运动引起Er的变化形式Eθ、加速运动电荷o产生的引力场A三者之间的关系。

2.加速运动点电荷的变化磁场产生引力场

按照麦克斯韦方程，电场在真空中变化，必然产生变化的磁场。

统一场论、相对论都认为，电荷o以速度V运动的时候，电场E和磁场B满足一种基本关系：

B = E ×V/ c²

因为电荷加速运动而变化产生的横向电场Eθ和变化产生的横向磁场Bθ所满足的关系，没有跳出B = E ×V/ c²

只是这个时候，运动速度V不是电荷的运动速度，而是加速电荷产生横向电场和横向磁场的传播速度，这个传播速度也就是电磁波【电磁波的本质就是加速电荷产生横向电场和垂直方向上的横向磁场】的传播速度，也就是矢量光速C。

所以有式：

Bθ = C×Eθ / c²

c Bθ = Eθ

上式和式Eθ/er = R×A/c² 【注意，er是Er的数量】比较，我们有：

Bθ/er= R×A/c³

上式表示了电荷本来存在的电场Er【数量为er】因为电荷直线加速运动而变化，所产生的引力场A、变化磁场Bθ三者之间的关系。

以上描述了电荷加速运动，引起电场变化，产生了变化磁场和引力场，并且给出了加速变化电场、加速变化磁场、引力场三者相互关系【包含了方向】。